The middle-square method is a method of generating pseudorandom numbers.

According to Wiki, the method was invented by John von Neumann, and was described at a conference in 1949.

So this is a pretty primitive pseudorandom generator algorithm. But it is also a good starting point for learning how to generate pseudorandom numbers by hand.

The Algorithm's process is very simple. The input is just a number, called the seed, which is used as the starting point. And then we do a square of the seed, and slice the middle part. This is the output and we also use this output for generate next random number.

Below image I take from Wiki shows the process very well.

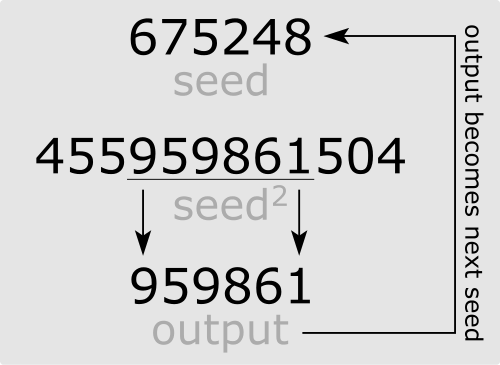
One thing needed to be considered is that if the number of digit of the seed is odd, then we need to make it even. For example, if the number of digit of the seed is 3, then after square, digits number becomes 6(max). Then we can't slice 3 digits in the middle, because either way digits number of left or right part is not equal.

Below is the simple code demo of this algorithm.

class RandomGenerator {
    private n: number;
    private seed: number;

    constructor(seed: number) {
        this.seed = seed;
        let n = seed.toString().length;
        if (n % 2 === 1) {
            n += 1;
        }
        this.n = n;
    }

    random() {
        let vStr = (this.seed * this.seed)
            .toString()
            .padStart(this.n, "0")
            .slice(this.n / 2, this.n / 2 + this.n);
        this.seed = parseInt(vStr);
        return this.seed;
    }
}

const rg = new RandomGenerator(1234);
for(let i = 0; i < 20; i++) {
    console.log(rg.random())
}