In this article, let's solve the leetcode Diagonal Traverse problem.

The image below shows what the problem requires. We need to traverse the 2-dimensional array diagonally to get a 1-dimemsional array.

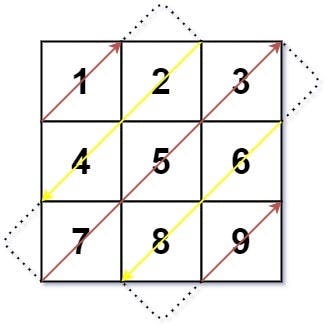
We could follow what the problem says, simulate the process to get the output. But I found that's too boring. Then I found a solution which is very clever. Let's me use this algorithm to solve this problem.

Let's consider this 2-dimensional array.

1 2 3 
3 4 5 
7 8 9

Express this array using element's indices.

[
    (0,0), (0,1), (0,2),
    (1,0), (1,1), (1,2),
    (2,0), (2,1), (2,2),
]

Group them diagonally, as the problem says.

[
    [(0,0)],
    [(0,1),(1,0)],
    [(0,2),(1,1),(2,0)],
    [(1,2),(2,1)],
    [(2,2)]
]

What pattern do you see? Yes, if the sum of the indices are the same, then they belong to the same group.

So now we can get groups one by one. One last thing to do, we need to adjust the direction. This is simple too. If the array's index is even, then reverse them.

That's all the process, let's see the code.

function findDiagonalOrder(mat: number[][]): number[] {

    // grouping array
    let groups: number[][][] = Array.from({ length: mat.length + mat[0].length - 1 }, _ => []);
    for (let i = 0; i < mat.length; i++) {
        for (let j = 0; j < mat[i].length; j++) {
            groups[i + j].push([i, j]);
        }
    }

    let result: number[] = [];
    for (let i = 0; i < groups.length; i++) {
        if (i % 2 === 0) {
            groups[i].reverse();
        }
        for (let j = 0; j < groups[i].length; j++) {
            result.push(mat[groups[i][j][0]][groups[i][j][1]]);
        }
    }

    return result;
};