Inorder Traversal

The problem is to do an inorder traversal.

This is a pretty standard operation for tree structure. The most simple solution is to use recursion.

function walk(node: TreeNode | null, result: number[]) {
    if (node === null) return;
    walk(node.left, result);
    result.push(node.val);
    walk(node.right, result);
}


function inorderTraversal(root: TreeNode | null): number[] {
    let result: number[] = [];
    walk(root, result);
    return result;
};

Note that in the walk function, we first access all left tree, then access node's val, then access right tree. So in the recursion process, we actually use the recursive stack to store all the to be accessed current nodes.

Or we can use a hand created stack to store the to be accessed left nodes, so we can avoid the problem of recursion stack limit.

function inorderTraversal(root: TreeNode | null): number[] {
    let stack: TreeNode[] = [];
    let result : number[] = [];
    let current = root;
    while(current !== null || stack.length > 0) {
        while(current !== null) {
            stack.push(current);
            current = current.left;
        }
        current = stack.pop();
        result.push(current.val);
        current = current.right;
    }

    return result;
};

Threaded Tree

In typical tree structure, each node has a left and right pointer, which points to the left subtree's root and the right subtree's node. These 2 points can be null, which means it's a leaf node. So the structure is like below.

class TreeNode {
    val: number;
    left: TreeNode | null;
    right: TreeNode | null;
    constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
        this.val = (val === undefined ? 0 : val);
        this.left = (left === undefined ? null : left);
        this.right = (right === undefined ? null : right);
    }
}

For leaf nodes, its left and right pointer are all null. This is wasteful. The idea of threaded tree is to use these pointers to store additional information to help to speed up the tree traversal process.

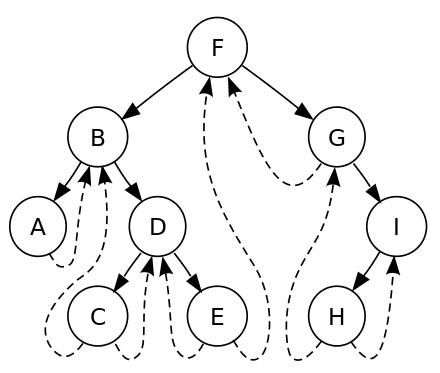
Specifically, for each leaf node, in threaded tree, we store its left node with the previous node in inorder traversal, and store its right node with the next node in inorder traversal. So the picture should looks like below. The part of the dotted line is the additional data we are talking about.

Morris Traversal

So how to implement the threaded tree? That's what morris traversal is. Not only we can use the morris traversal to implement the threaded tree, but also its process is actually can be use to do inorder traversal.

Before we go the the traversal details, let's consider its idea first. Remember in the inorder traversal, we need to use a stack to store all the nodes which will be accessed later. For example, say we are standing on the current node. If this node has left tree, then we should access its left tree first. But we also want to access current node when the left tree's traversal is done. So what we do is to push this current node into stack and pop it out when we need it.

In morris traversal, we don't use this stack. Remember in threaded tree, we use leaf node's left and right null pointers to store additional information. So in morris traversal, we use each leaf node's right pointer and points to the next node in inorder traversal. So in stack solution, whenever we access a leaf node, we will pop out a new node to access. Now in morris traversal, whenever we access a leaf node, we access its right pointer, which should be the next node in inorder traversal.

So how to achieve this? Say we are standing on current node. Then we should find the its previous node in inorder traversal and make its right pointer points to current node. Then how to find this previous node? Well, in inorder traversal, this previous node is current node's left tree's rightmost node.

For example, if current node is 1, then its previous node in inorder traversal is 5.

       1
     /   \
    2     3
   / \   /
  4   5 6

OK, with this in mind, what we will do is if current node has left tree, then find its previous node, make its previous node points to itself and if not, then access its right node directly. Let's see this in code.

function inorderTraversal(root: TreeNode | null): number[] {
    let result: number[] = [];
    let node = root;
    while(node) {
        if (node.left) {
            // if left tree exists
            // find previous node(its left tree's right most node)
            let preNode = node.left;
            while(preNode.right) {
                preNode = preNode.right;
            }
            // make this previosu node points to node
            preNode.right = node;

            // make current node's left as null to avoid infinity loop
            // current node goes to left
            const temp = node.left;
            node.left = null;
            node = temp;
        } else {
            result.push(node.val);
            node = node.right;
        }
    }
    return result;
};