In this article, let's try to sovle the leetcode problem Rotate Image.
As the problem requires, the operation is very much like a rotation. We can think of the matrix as an image and we need to rotate the image by 90 degrees (clockwise).
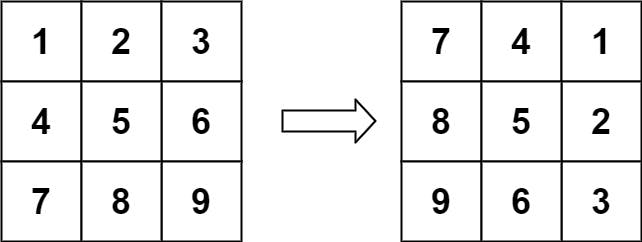
The rotation operation is easy, what makes this problem harder is that we need to do it in-place. So we need to figure out a way to store the temporary state within the matrix. Let's see an example.
Suppose the matrix is below.
1 2 3
4 5 6
7 8 9
To find out a pattern, let consider only the first value.
move 1 to target place
1 x 3 1 x 1
x x x => x x x
7 x 9 7 x 9
The value replaced by 1 is 3, let see where 3 goes.
1 x 1 1 x 1
x x x => x x x
7 x 9 7 x 3
Follow the same pattern.
1 x 1 1 x 1 7 x 1
x x x => x x x => x x x
7 x 3 9 x 3 9 x 3
Now you can see that we finished one rotation for the first value. For every step, we only need one variable to store the previous number.
Same pattern goes with other values. We can just follow this pattern to iterate all values to solve this problem. The visualization and code in leetcode describe this solution very well.
But this is not what this article for. I'm interested with this problem is because it is can be solved by classic matrix operation: transpose and reflect.
Matrix transpose is an operation to make each row to be each column. Below show that first row 1,2,3 becomes first column 1,2,3. Same things goes with other rows.
[
[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
]
transpose
[
[1, 4, 7],
[2, 5, 8],
[3, 6, 9],
]
Well, then how to do transpose in code? This seems pretty complicated as well. Instead of values, let's write all coordinates to see if there is a pattern.
[
[(0,0), (0,1), (0,2)],
[(1,0), (1,1), (1,2)],
[(2,0), (2,1), (2,2)],
]
transpose
[
[(0,0), (1,0), (2,0)],
[(0,1), (1,1), (2,1)],
[(0,2), (1,2), (2,2)],
]
As you can see, if current cell's index is (i,j), to do transpose we can just swap its values with index (j,i). But we need to be careful about this. We don't need to do it for every value, because in that case we will do swap twice. Actually, we only need to do swap for below values.
[
[ (1,0), (2,0)],
[ (2,1)],
[ ],
]
OK, that's clear now. Let's do transpose in code.
function transpose(matrix: number[][]): void {
for (let i = 0; i < matrix.length; i++) {
for (let j = i + 1; j < matrix.length; j++) {
[matrix[i][j], matrix[j][i]] = [matrix[j][i], matrix[i][j]];
}
}
}
Then what is reflect? We can think of reflect as a mirror effect. We can choose to do reflect by x axis or y axis. Below shows the process of reflect by y axis.
[
[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
]
reflect
[
[3, 2, 1],
[6, 5, 4],
[9, 8, 7],
]
Well, this seems easy. What we only need is to swap columns on the left with columns on the right. Let's see it in code.
function reflect(matrix: number[][]): void {
const mid = Math.floor(matrix.length / 2);
for (let i = 0; i < matrix.length; i++) {
for (let j = 0; j < mid; j++) {
[
matrix[i][j],
matrix[i][matrix.length - j - 1]
] = [
matrix[i][matrix.length - j - 1],
matrix[i][j]
];
}
}
}
OK, now we know how to do transpose and reflect on matrix. How these can be of help for solving this problem? Well, let's see the process in below.
1 2 3
4 5 6
7 8 9
transpose =>
1 4 7
2 5 8
3 6 9
reflect =>
7 4 1
8 5 2
9 6 3
So, what we only need to do is one transpose and one reflect, then problem solved.
function rotate(matrix: number[][]): void {
transpose(matrix);
reflect(matrix);
};

