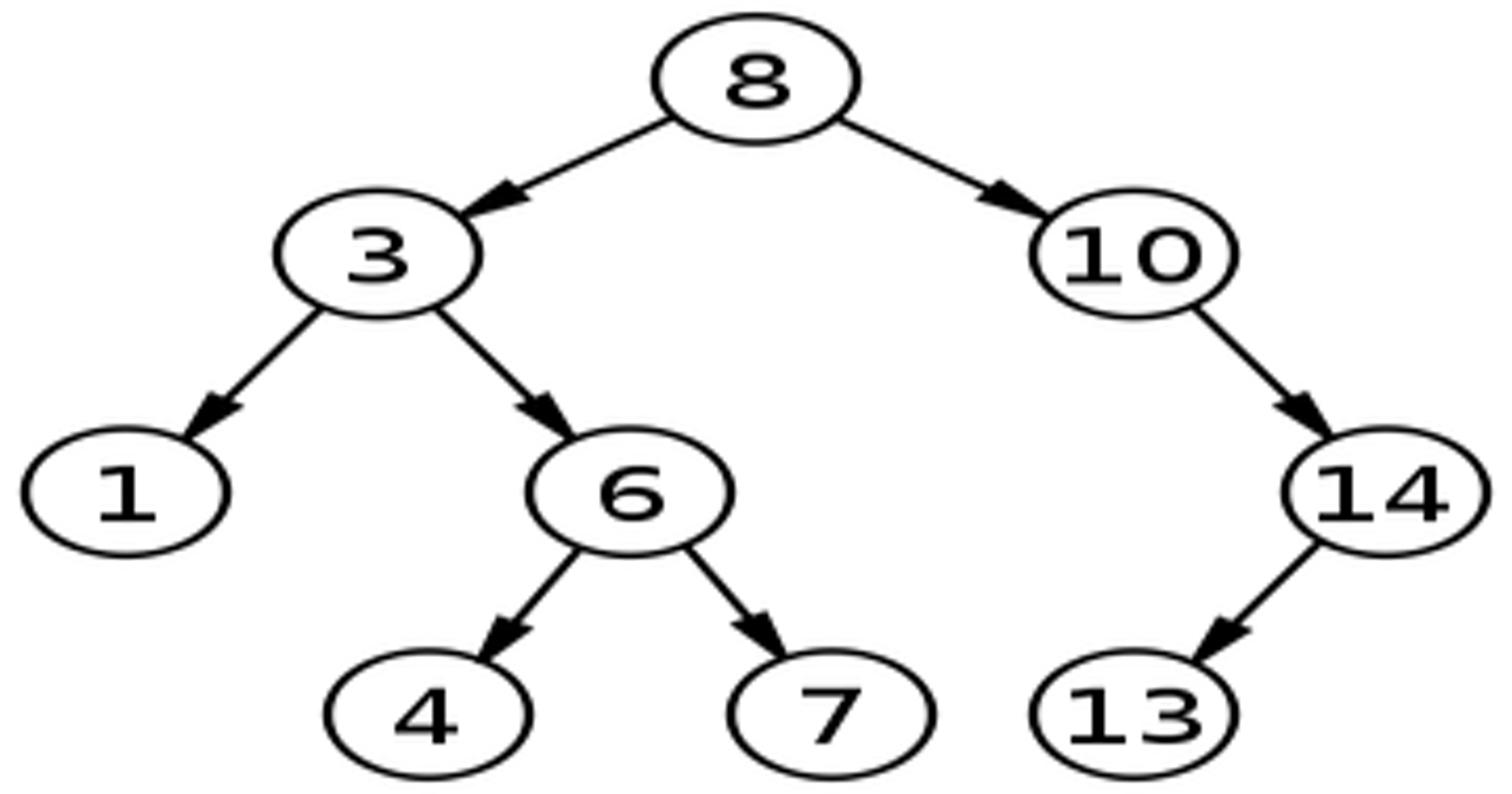
A binary search tree (BST) is a binary tree which each node's value larger than its left tree's node's values, and less than its right tree's node's values.

Below image (from wiki) shows a binary tree.

Tree node structure is the same as a normal binary tree.

class TreeNode {
    val: number;
    left: TreeNode | null;
    right: TreeNode | null;
    constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
        this.val = (val === undefined ? 0 : val);
        this.left = (left === undefined ? null : left);
        this.right = (right === undefined ? null : right);
    }
}

With binary search tree, we can achieve average O(log(n)) time complexity for searching, inserting and deleting operations.

Search and Insert in BST is easy, just start from the root node, and go down left if current value is less than node's value, or go right.

The delete operation of BST is relatively complicated. Because after deleting, we need to make sure the binary tree is still a valid BST.

Before we see how to delete node in a BST, let's first consider how to delete node in a normal binary tree.

The binary tree data structure is a recursive structure, so its good to do delete operation recursively. Specifically, for each recursive step, if current node is null, return null. If current node's is the target node, then return current node's child(left or right all ok). If all not, then do this step recursively on child nodes.

function deleteNode(root: TreeNode | null, key: number): TreeNode | null {
    if (root === null) return null;

    if (root.val === key) {
        return root.left;  // or right
    }

    root.left = deleteNode(root.left, key);
    root.right = deleteNode(root.right, key);

    return root;
};

Now we know how to delete a node in a normal binary tree, let's consider how to delete a node in a BST. There are 3 cases we need to consider.

First, if target node is a leaf node, then just delete this node, the tree will still be a BST.

Second, if target node only have one child, then what we need to do is, delete target node, and make target node's parent point to target node's only child.

The third case is most complicated, if target node have both left child and right child, what do we do?

To figure out the solution, we need to go back to the definition of the BST. In a BST, every node's value is bigger than it's left trees, and less than its right trees. After deleting the target node, what we need to do is to find a replacement to sit on the target node's seat and make sure the tree is still a BST.

Because now we have both left tree and right tree, so actually, we have 2 options to select the replacement:

1. find the largest node in left tree
2. find the smallest node in right tree

Take option 1 as an example. We make the largest node in left tree sit on the target node's original seat. It's already the largest node in left tree, so left part is ok. It's from left tree, so it is definately less than all right tree. So right part is ok.

Now the question is, how to find the largest node in left tree(take option 1 as an example, same logic for option 2). The answer is simple. In BST, the right node is always bigger, so we loop down the right, the rightest leaf node of left tree is the largest node in left tree.

Now its the time to see the code. Don't forget test it in leetcode Delete Node in a BST.

function deleteNode(root: TreeNode | null, key: number): TreeNode | null {
    if (root === null) return null;

    if (root.val < key) {
        root.right = deleteNode(root.right, key);
        return root;
    } if (root.val > key) {
        root.left = deleteNode(root.left, key);
        return root;
    } else {
        if (root.left === null) {
            return root.right;
        }
        if (root.right === null) {
            return root.left;
        }

        // find largest value in left child tree
        let leftLargestNode = root.left;
        while (leftLargestNode.right !== null) {
            leftLargestNode = leftLargestNode.right;
        }

        // delete it
        deleteNode(root, leftLargestNode.val);

        // make it point to target node's children
        leftLargestNode.left = root.left;
        leftLargestNode.right = root.right;

        // return it to target node's parent
        return leftLargestNode;
    }
};