Binary Search

Given an array of integers nums which is sorted in ascending order, and an integer target, write a function to search target in nums. If target exists, then return its index. Otherwise, return -1.

We can just iterate the array to find the target, but in this way, the time complexity would be O(n). To make it O(log(n)), we need to use binary search. The idea is simple, since the array is sorted in ascending order, every time we can check the middle value with the target value. So every iteration, we can drop half of the array, so time complexity becomes O(log(n)).

function search(nums: number[], target: number): number {
    let low = 0;
    let high = nums.length - 1;

    while (low <= high) {
        const mid = ((high - low) >> 1) + low;
        if (nums[mid] === target) {
            return mid;
        }
        if (nums[mid] < target) {
            low = mid + 1;
            continue;
        }
        if (nums[mid] > target) {
            high = mid - 1;
            continue;
        }
    }
    return -1;
};

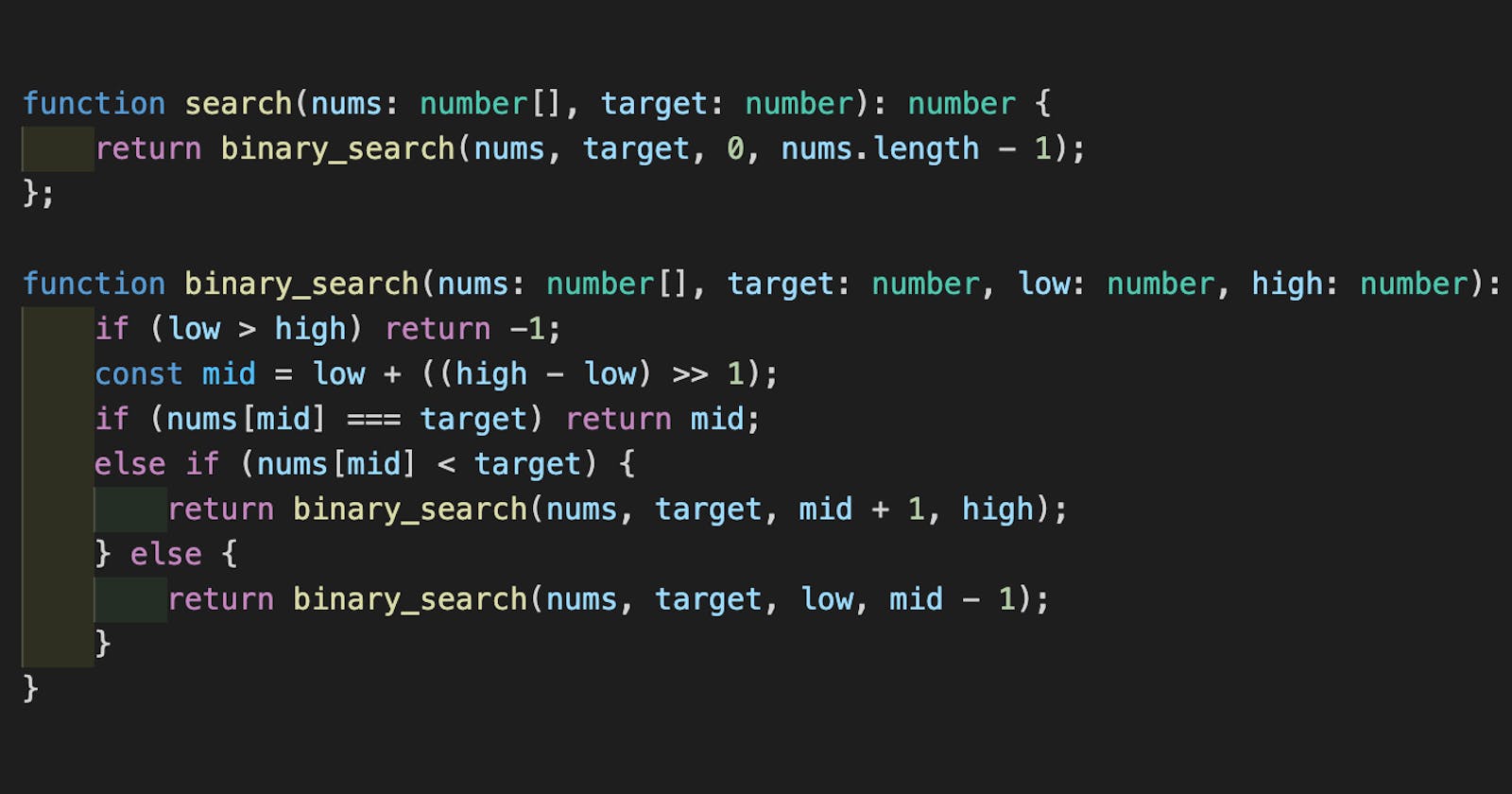
The above code is the iterative method, we can also do it recursively.

function search(nums: number[], target: number): number {
    return binary_search(nums, target, 0, nums.length - 1);
};

function binary_search(nums: number[], target: number, low: number, high: number): number {
    if (low > high) return -1;
    const mid = low + ((high - low) >> 1);
    if (nums[mid] === target) return mid;
    else if (nums[mid] < target) {
        return binary_search(nums, target, mid + 1, high);
    } else {
        return binary_search(nums, target, low, mid - 1);
    }
}

Search in a Sorted Array of Unknown Size

You have a sorted array of unique elements and an unknown size. You do not have an access to the array but you can use the ArrayReader interface to access it. You can call ArrayReader.get(i) that.

In binary search, we need to know the left and right boundaries to get the middle value. But how can we do it for unknow size array? The idea is to find the boundaries first, then run the binary search. But how to find the boundaries? Remember we need to do the whole search in O(log(n)), so we can't iterate the while array either. We could start from 1 and increate it exponentially, until we find the right boundary.

class ArrayReader {
    // This is the ArrayReader's API interface.
    // You should not implement it, or speculate about its implementation
    get(index: number): number {
        return 0;
    };
};


function search(reader: ArrayReader, target: number): number {
    let l = 0;
    let r = 1;
    while (true) {
        const v = reader.get(r);
        if (v >= target) {
            break;
        }
        l = r + 1;
        r *= 2; // increate exponentially
    }
    return binary_search(reader, l, r, target);
};


function binary_search(reader: ArrayReader, l: number, r: number, target: number): number {
    if (l > r) return -1;
    const mid = l + ((r - l) >> 1);
    const v = reader.get(mid);
    if (v < target) {
        return binary_search(reader, mid + 1, r, target);
    } else if (v > target) {
        return binary_search(reader, l, mid - 1, target);
    } else {
        return mid;
    }
};